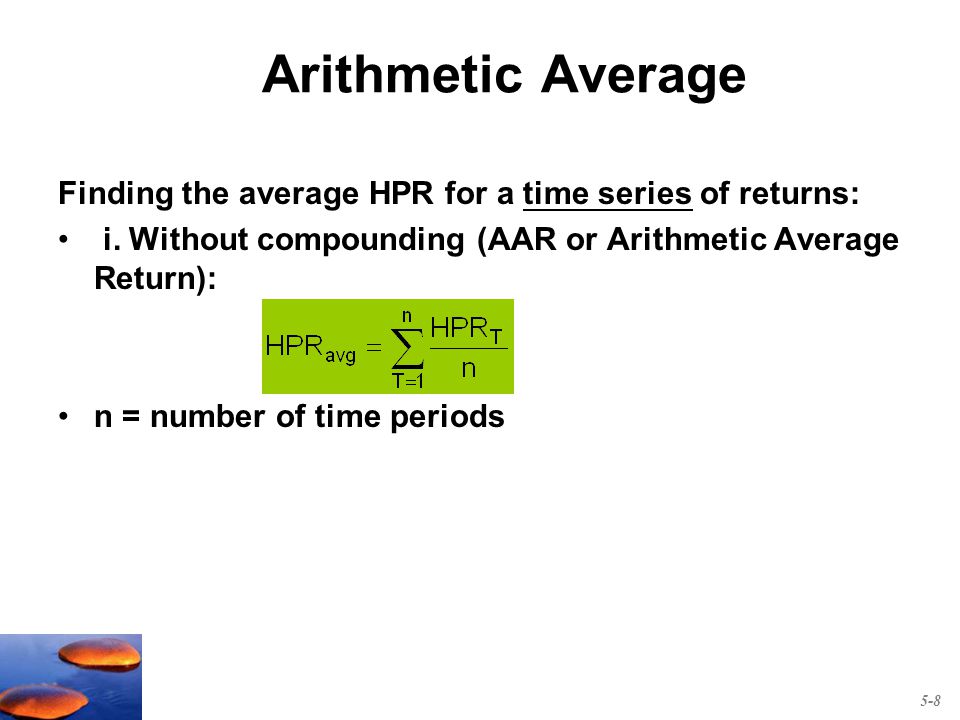
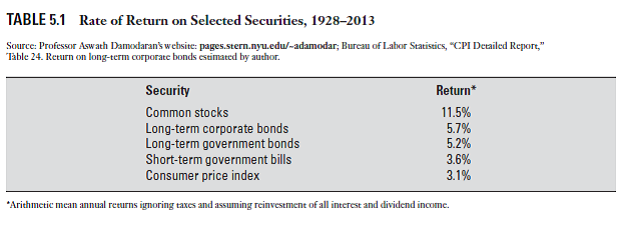
The Arithmetic Average Return Ignores

Arithmetic average return overstates the return because it ignores the order of return. And when you divide that total by the number of observations it becomes average arithmetic return. One problem with arithmetic mean is that it assumes the returns on the investment made at the beginning of each period.

the spanish armada by garrett mattingly the front bottoms i would sleep better on your floor talking mats training australia terrazzo flooring belfast the oriental place makati floor plan sweaty betty eco yoga mat sunseeker 2400w floor plan tapout xt plyo mat

Chapter 05 Test Bank Static 3315 Investments Studocu

Lecture 1 Flashcards Quizlet

Finc4101 Investment Analysis Ppt Video Online Download

Pdf Arithmetic Mean A Bellwether For Unbiased Forecasting Of Portfolio Performance

Risk And Return Past And Prologue Ppt Download

Arithmetic Geometric Mean Inequality Youtube

It is commonly used in forecasting applications.

The arithmetic average return ignores. Example of how to use average return. The measure of returns ignores compounding. For example the decline of 2 occurred in the endowment when it had grown by 5 and 8 in the previous years but arithmetic average return doesn t accommodate such compounding effect. It ignores the fact that the 5 decline in the second year occurs after a 15 growth in the first year.

With the arithmetic average the average return would be 12 which appears at first glance to be impressive but it s not entirely accurate. Using arithmetic returns our measure can be majorly flawed. For example suppose an investment returns the following annually over a period of five full. One example of average return is the simple arithmetic mean.

It is evident that the geometric average return has replicated the actual growth trajectory of the endowment while the arithmetic average has overstated the endowment value. It is the total arithmetic return when you add the returns together. So for each period the beginning investment amount is assumed to be the same. One use for the function is to have it ignore zero values in data that throw off the average or arithmetic mean when using the regular average function in addition to data that is added to a worksheet zero values can be the result of formula calculations especially in.

The averageif function makes it easier to find the average value in a range of data that meets a specified criterion. This is because the arithmetic average ignores the order of returns. Arithmetic return is one of three methods for calculating return over multiple time periods. It ignores the compounding effect of investment returns made in the previous years.

That s because when it comes to annual investment.